Stirling Engine Analysis 

What is the total work done in one cycle? 

Using the compression ratio, minimum and maximum temperatures, and stroke length, we can get a more accurate calculation. Since we know V1=V4=166.499 cm3V2=V3=163.501 cm3T1=T2=295.15 KT3=T4=313.45 K, we can calculate Wnet=0.095245 kJ/kg. The efficiency is calculated at =0.0583, or 5.83%. The mass of air is in the can is calculated to be m=165*10-6*1.225=.000202 kg. That means total work done in one cycle is W=0.095245*.00202=0.019251 J.

What is the net force generated by the engine?

We will now calculate the force the cycle outputs to see if it can lift the quarter or not. Our corrected stroke length is 1 in. One cycle is equivalent to two strokes, so the cycle length is 2 in. Work is equal to force times displacement, where displacement is the cycle length, so here force F=Wd=.0192512*39.37=.379 N. In the first report, we determined the force needed to lift quarter to be .0556 N, so this engine produces more than enough force to do that. The net force the engine generates is Fnet=.379-.0556=.323 N. We assumed the temperature of the can is equal to the temperature of the air inside. In reality, the air temperature will be lower since air has its own specific heat. This means the actual temperature difference will be lower and thus, a lower engine efficiency.

Temperature Gradient 

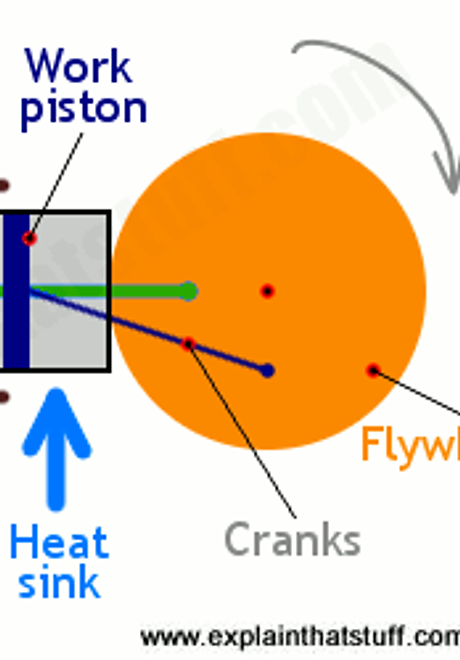
The efficiency of the heat engine is only affected by the temperature difference between the expansion and compression cycles of the Stirling engine. The initial temperature is primarily controlled by the ambient temperature, but it can be lowered if a fluid or another cooling method is used to reduce the temperature at cold side of the Stirling engine, while the hot side can only be increased by adding more heat from the candle. The efficiency of this engine model can also be affected by other factors such friction between the steel wool piston/regenerator, and heat lost between the hot and cold side of the cylinder.